什么是汉诺塔？

目标

• 有三根杆子 A，B，C。 A杆 上有 个 穿孔圆盘，盘的尺寸由下到上依次变小。要求按下列规则将所有圆盘移至 C杆 。

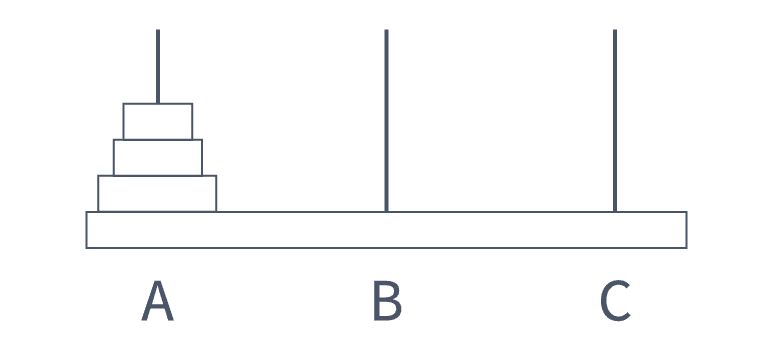
规则

1. 每次只能移动 1 个圆盘；
2. 大盘不能叠在小盘上面。

问题

• 如何移动？
• 最少移动几次？

分情况讨论

• 按照递归的惯例，我们先从递推，即第 1 种情况、第 2 种情况等，到递归。所以我们现在来看具体的情况。

• 在那之前，我们需要定义一个函数，方便思考：TOH(n, from, via, to)

  • n 为初始的穿孔圆盘数量。

  • A，B，C 分别从左到右代表 3 根柱子。

    A	B	C
    1	2	3

  • from, via, to 输入的是柱子的序号，意思是从 from 通过 via 移动到 to。

    • 例如从 A 通过 B 移动到 C 则表示为 TOH(n, A, B, C)

情况 #1 - 1 个穿孔圆盘

• TOH(1, A, B, C)
• 第一种情况只需要将 A 移动 1 块到 C 即可。
• 为了统一函数的表示，我们这边假设需要使用到 B。

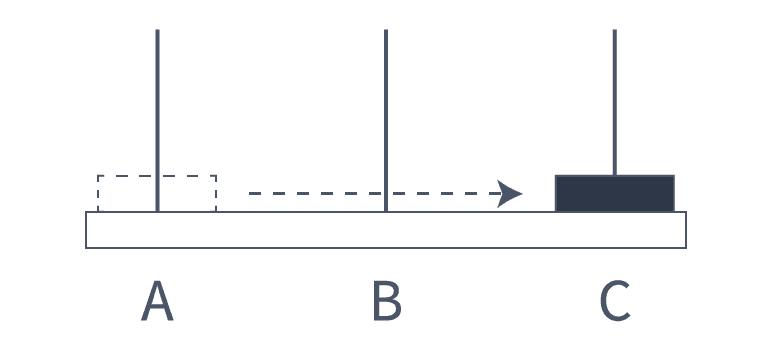
情况 #2 - 2 个穿孔圆盘

• TOH(2, A, B, C)
• 对于第 2 种情况，我们需要 3 步：
  1. A 移动 1 块到 B，即 TOH(1, A, C, B)。
  2. A 移动 1 块到 C。
  3. B 移动 1 块到 C，即 TOH(1, B, A, C)。

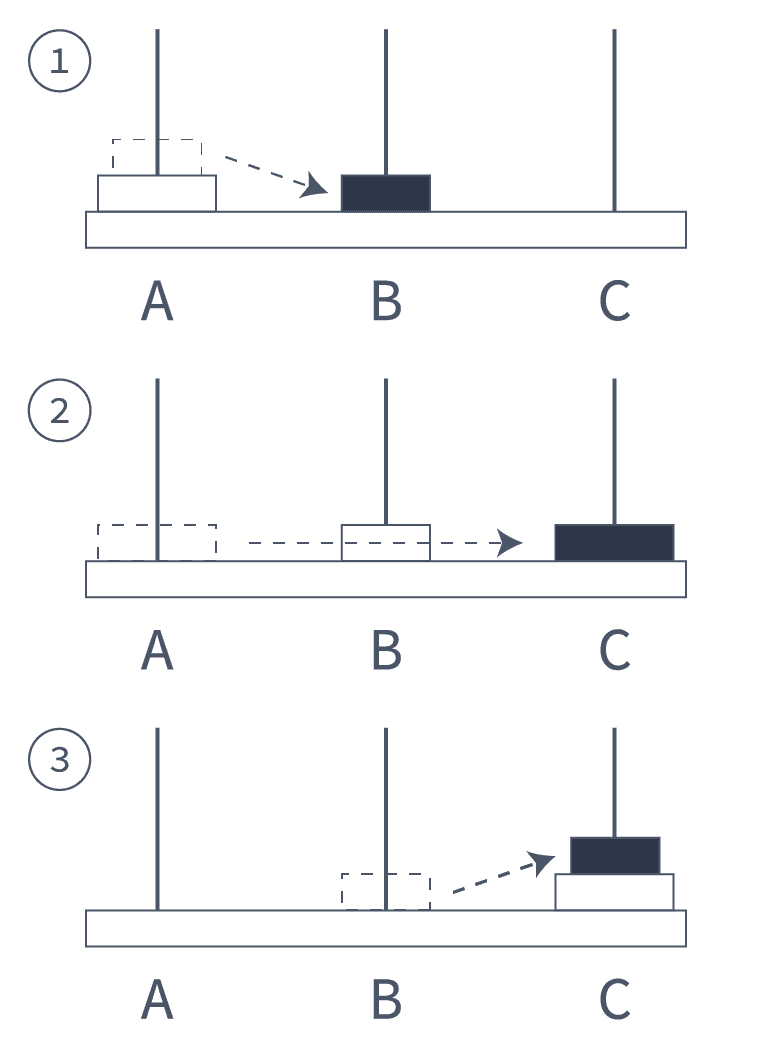
情况 #3 - 3 个穿孔圆盘

• TOH(3, A, B, C)
• 对于第 3 种情况，我们仍然需要“3”步：
  1. A 移动 2 块到 B，即 TOH(2, A, C, B)。
     • 这边并没有破坏只能移动 1 块的规则，而是把情况而重新做一遍。
  2. A 移动 1 块到 C。
  3. B 移动 2 块到 C，即 TOH(2, B, A, C)。

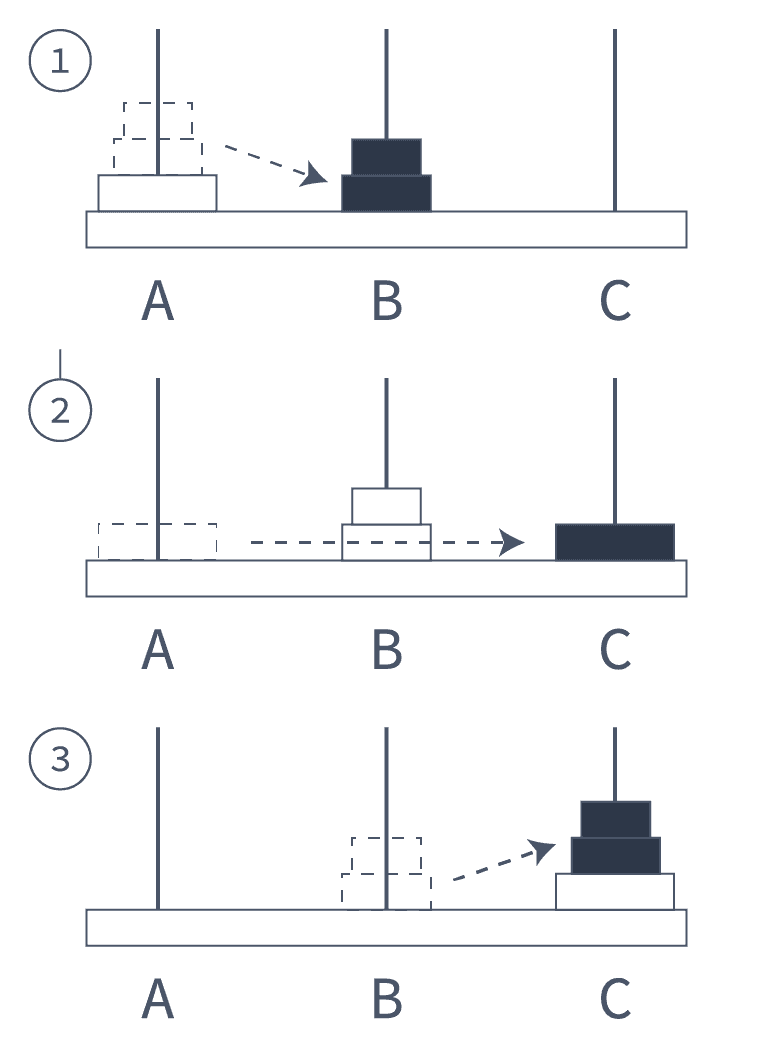
情况 #n - n 个穿孔圆盘

• TOH(n, A, B, C)
• 对于第 n 种情况，我们发现只要调用 n-1 的递归就好了：
  1. A 移动 n - 1 块到 B，即 TOH(n-1, A, C, B)。
  2. A 移动 1 块到 C。
  3. B 移动 n - 1 块到 C，即 TOH(n-1, B, A, C)。

代码

• 那么我们现在就可以写代码啦！

1
2void TOH(int n, int a, int b, int c)
3{
4if (n > 0)
5{
6// 1st step
7TOH(n - 1, a, c, b);
8// 2nd step
9printf("from %d to %d", a, c);
10// 3rd step
11TOH(n - 1, b, a, c);
12}
13}
14

递归树

• 我们解决了如何移动的问题，那么最少移动了几次呢？我们观察递归树就可以知道了：

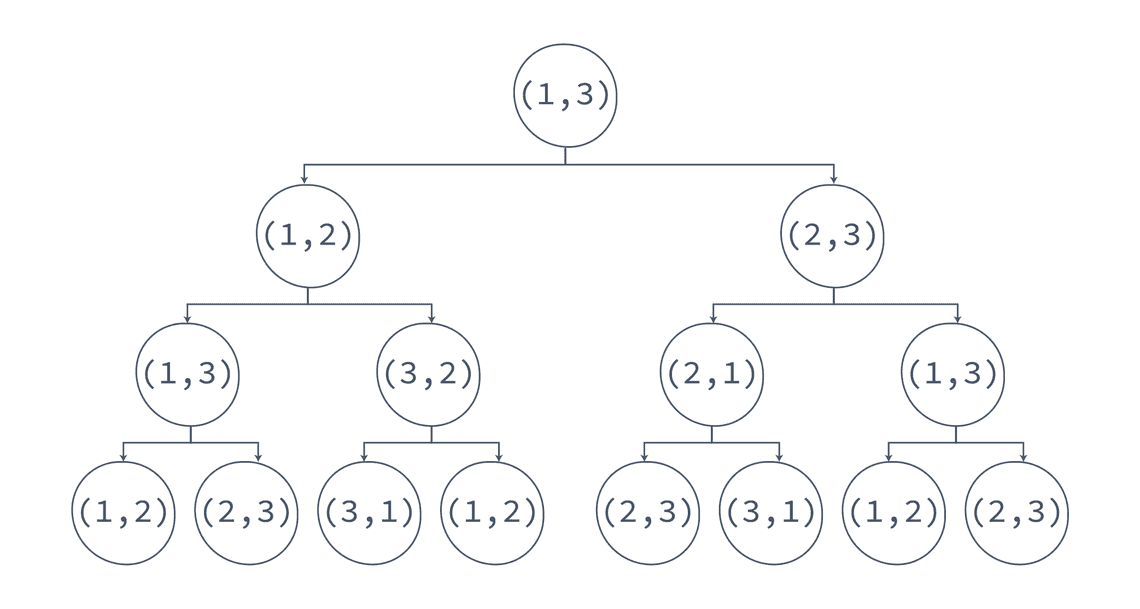
• 根据上图，我们得知：
  • 对于 TOH(2) ，函数一共调用了 7 次，即 。
  • 对于 TOH(3) ，函数一共调用了 15 次，即 。
• 细心的你一定发现了，这与 n 位比特位（2 进制）能表达的最大值一样，即对于 TOH(n) 我们需要 次移动。
• 如此一来，我们就完全解决了汉诺塔的问题。